待完善

工作中需要检测服务所用的TLS套件版本等，可以用以下几种工具

环境：centos 7

nginx 版本：1.19.1

1 https

SSL(Secure Sockets Layer) 安全套接层，是一种安全协议，经历了 SSL 1.0、2.0、3.0 版本后发展成了标准安全协议 - TLS(Transport Layer Security) 传输层安全性协议。TLS 有 1.0 (RFC 2246)、1.1(RFC 4346)、1.2(RFC 5246)、1.3(RFC 8446) 版本。

二分查找也称折半查找（Binary Search），是一种在有序数组中查找某一特定元素的搜索算法。我们可以从定义可知，运用二分搜索的前提是数组必须是有序的，这里需要注意的是，我们的输入不一定是数组，也可以是数组中某一区间的起始位置和终止位置

栈先进后出，队列先进先出。

1 剑指 Offer 09. 用两个栈实现队列

题目描述

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

输入：
[“CQueue”,”appendTail”,”deleteHead”,”deleteHead”]
[[],[3],[],[]]
输出：[null,null,3,-1]

解题思路

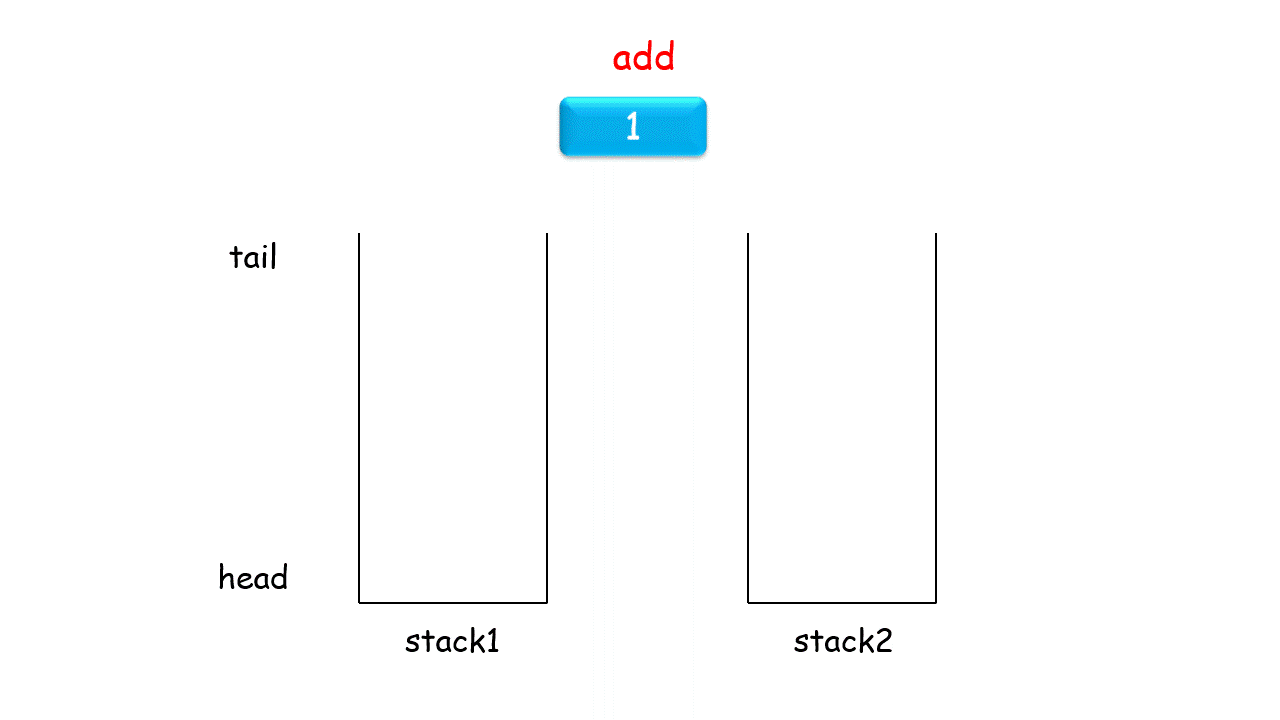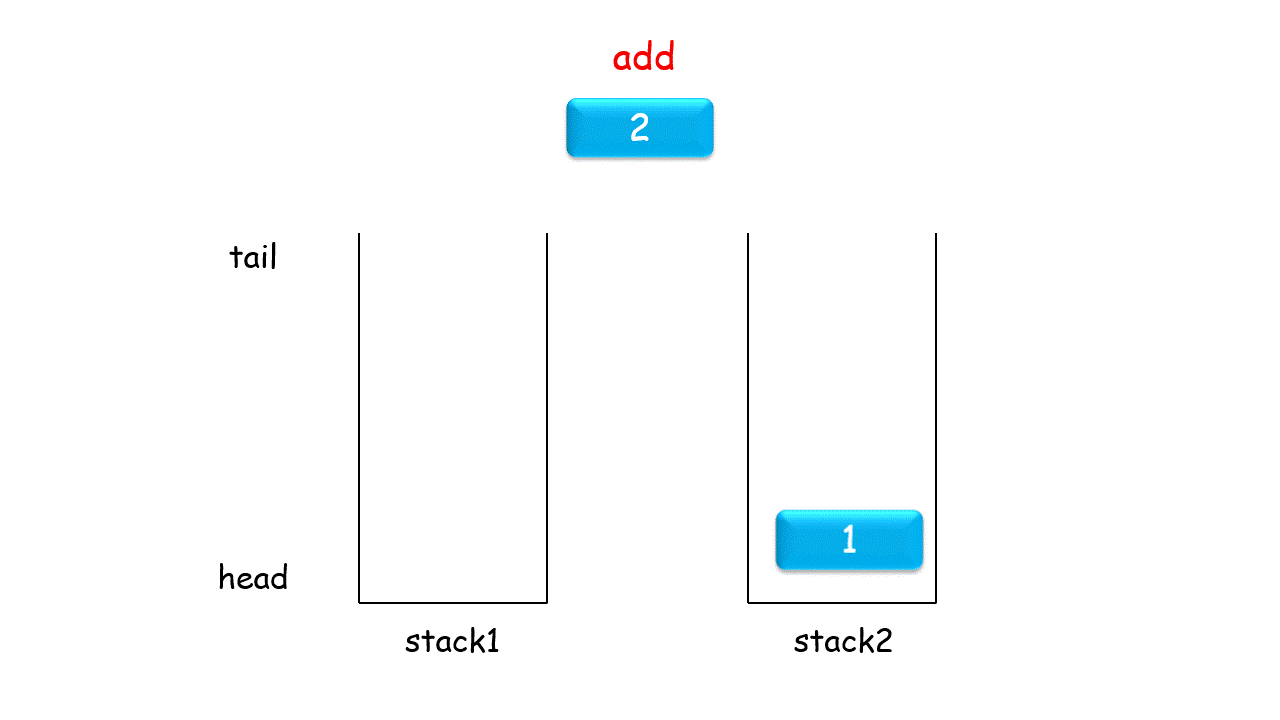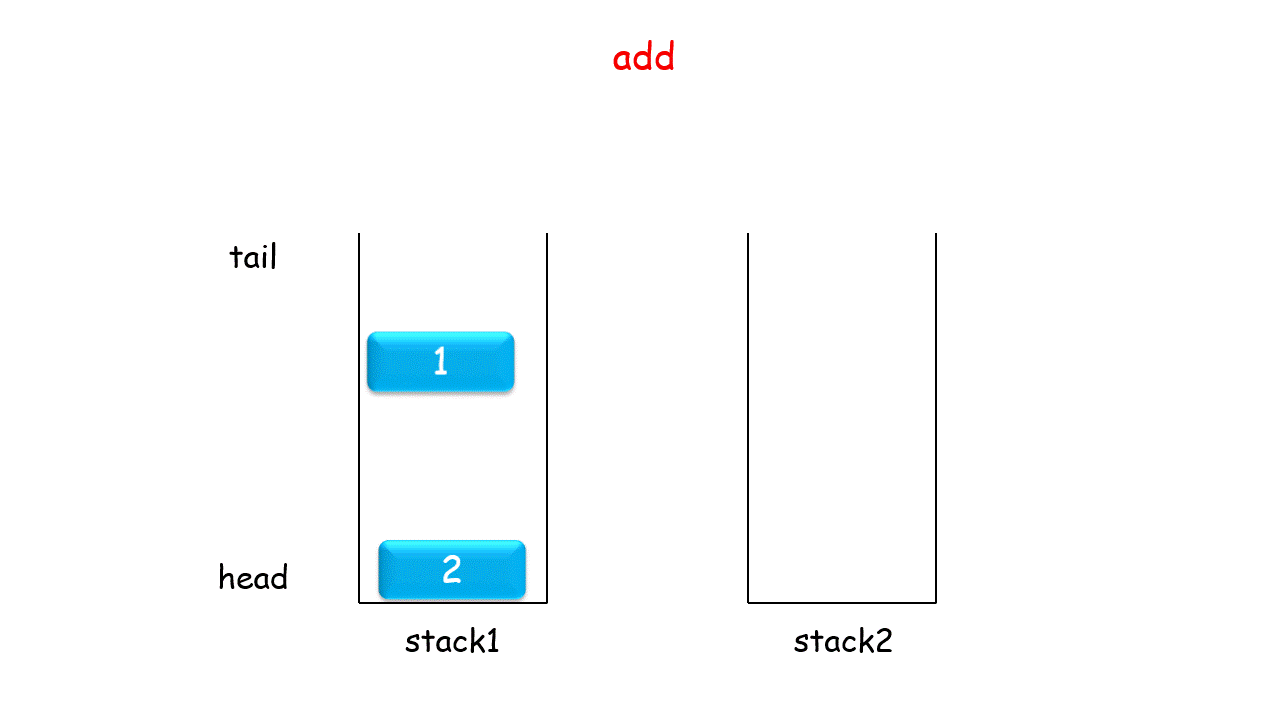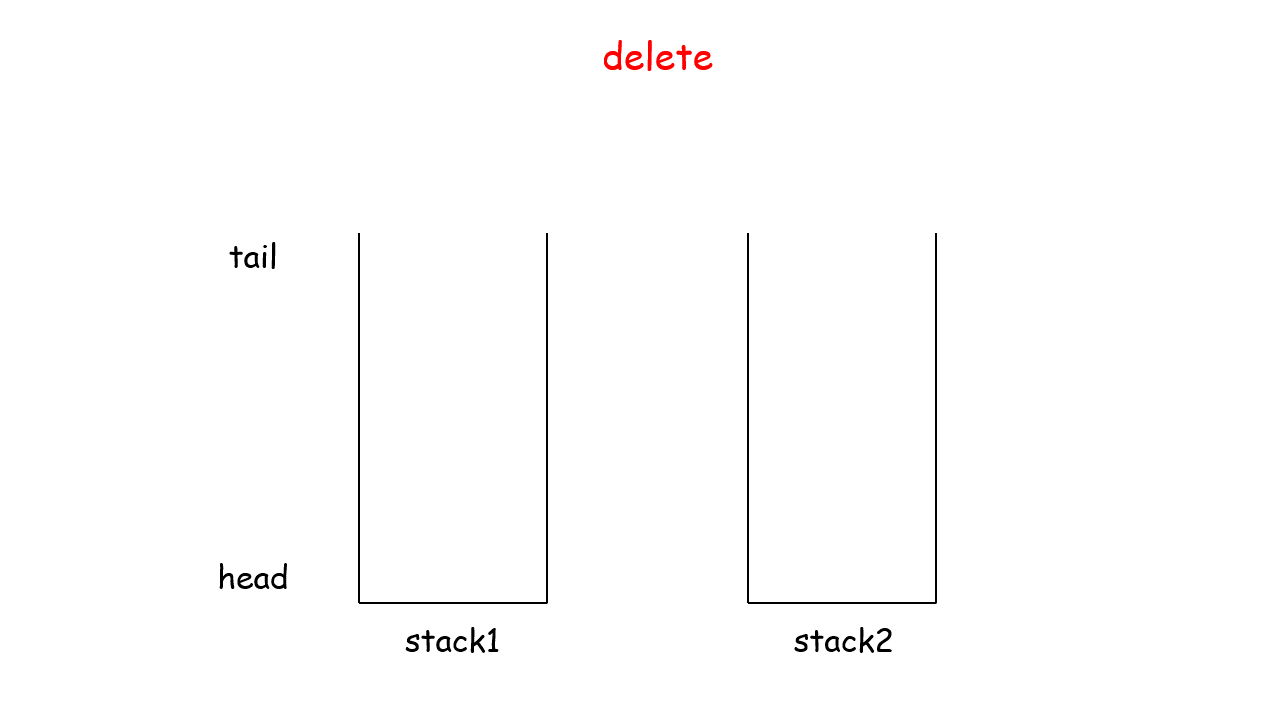
题目只要求实现 加入队尾appendTail() 和 删除队首deleteHead() 两个函数的正常工作，因此我们可以设计栈 A 用于加入队尾操作，栈 B 用于将元素倒序，从而实现删除队首元素。

加入队尾 appendTail()函数： 将数字 val 加入栈 A 即可。
删除队首deleteHead()函数： 有以下三种情况。
当栈 B 不为空： B中仍有已完成倒序的元素，因此直接返回 B 的栈顶元素。
否则，当 A 为空： 即两个栈都为空，无元素，因此返回 -1−1 。
否则： 将栈 A 元素全部转移至栈 B 中，实现元素倒序，并返回栈 B 的栈顶元素。

代码

# -*- coding: utf-8 -*-
class CQueue(object):
    def __init__(self):
        self.A=[]
        self.B=[]
    def appendTail(self, value):
        """
        :type value: int
        :rtype: None
        """
        self.A.append(value)
    def deleteHead(self):
        """
        :rtype: int
        """
        if self.B: return self.B.pop()#如果B栈有元素  则弹出栈顶元素即可
        if not self.A: return -1#B为空 并且A 为空  则返回-1
        #当A不为空的时候
        while self.A:
            self.B.append((self.A.pop()))#将A栈弹出  入B栈
        return self.B.pop()

复杂度分析

时间复杂度： appendTail()函数为 O(1) ；deleteHead() 函数在 N 次队首元素删除操作中总共需完成 N个元素的倒序。
空间复杂度： O(N)最差情况下，栈 A 和 B 共保存 N个元素。

2 leetcode225. 用队列实现栈

题目描述

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
[“MyStack”, “push”, “push”, “top”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

代码

class MyStack(object):
    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.A=deque()
        self.B=deque()
    def push(self, x):
        """
        Push element x onto stack.
        :type x: int
        :rtype: None
        """
        self.A.append(x)
    def pop(self):
        """
        Removes the element on top of the stack and returns that element.
        :rtype: int
        """
        size=len(self.A)-1#留一个元素
        while size>0:
            self.B.append(self.A.popleft())#将A的元素除了最左边的都弹入B中
            size=size-1
        res=self.A.popleft()#返回
        self.A,self.B=self.B,self.A##将que2和que1交换 que1经过之前的操作应该是空了
        #一定注意不能直接使用que1 = que2 这样que2的改变会影响que1 可以用浅拷贝
        return res
    def top(self):
        """
        Get the top element.
        :rtype: int
        """
        return self.A[-1]
    def empty(self):
        """
        Returns whether the stack is empty.
        :rtype: bool
        """
        if len(self.A)==0:
            return True
        else:
            return False

复杂度分析

时间复杂度：入栈操作O(n)，其余操作都是 O(1)。
入栈操作需要将A 中的 n个元素出队，并入队 n+1个元素到B ，共有 2n+1 次操作，每次出队和入队操作的时间复杂度都是 O(1)，因此入栈操作的时间复杂度是O(n)。
出栈操作对应将A的前端元素出队，时间复杂度是 O(1)。
获得栈顶元素操作对应获得 A的前端元素，时间复杂度是 O(1)。
判断栈是否为空操作只需要判断A是否为空，时间复杂度是 O(1)。

空间复杂度：O(n)，其中 n 是栈内的元素。需要使用两个队列存储栈内的元素。

3 leetcode 20. 有效的括号

题目描述

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串 s ，判断字符串是否有效。

有效000字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

示例 1：

输入：s = “()”
输出：true
示例 2：

输入：s = “()[]{}”
输出：true

解题思路

1.1 待入栈元素在字典中无匹配元素即都是左括号 则 入栈

1.2 若待入栈元素在字典中有匹配元素

​ 1.2.1 stack不为空（防止s=”]”的情况） 并且 在栈顶匹配元素成功

​ 则 将栈顶元素pop出

​ 1.2.2 否则 直接返回False

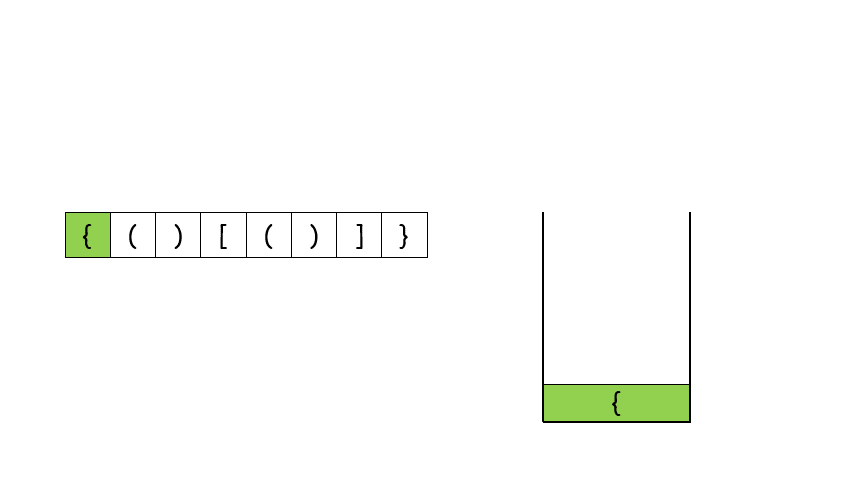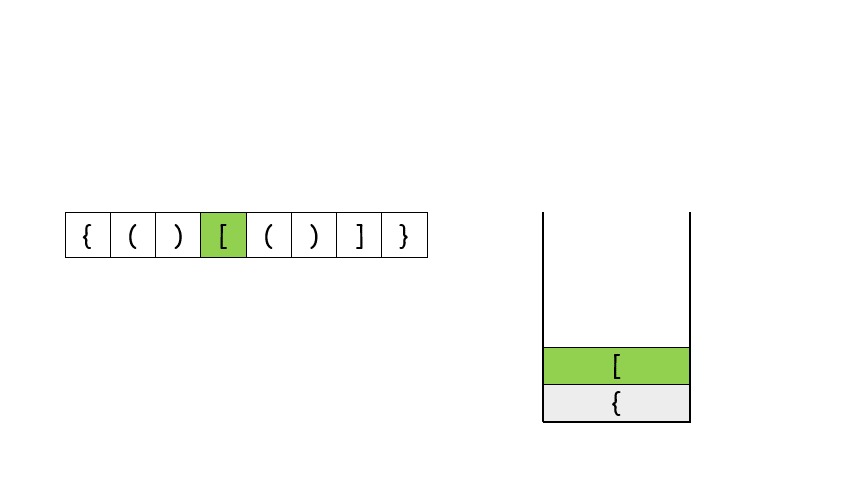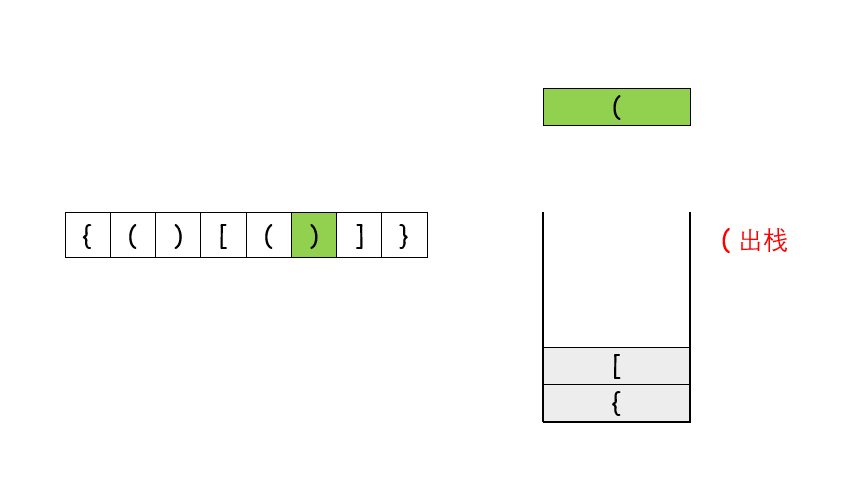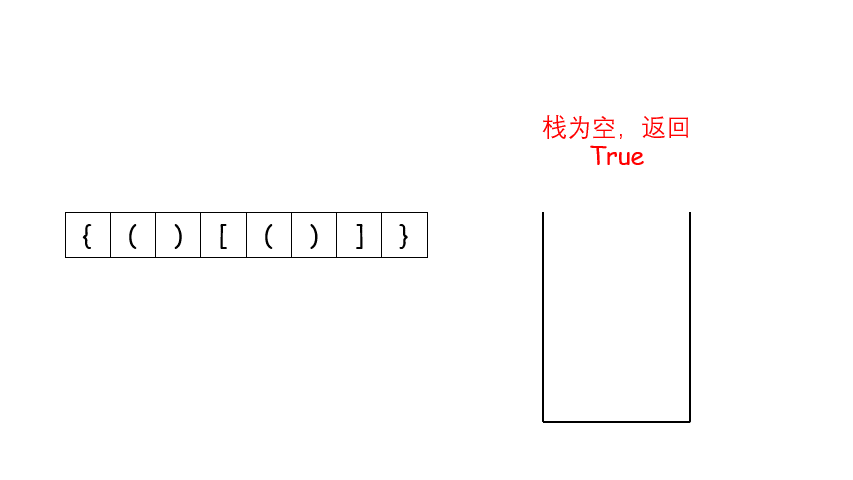
代码

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        dic={')':'(','}':"{","]":"["}
        stack=[]
        for i in s:
            if dic.get(i) is None:#待入栈元素在字典中无匹配元素即都是左括号 则 入栈
                stack.append(i)
            else:##若待入栈元素在字典中有匹配元素
                if  stack and stack[-1]==dic.get(i): #并且stack不为空（防止s="]"的情况） 在栈顶匹配元素成功 则 将栈顶元素pop出
                    stack.pop()
                else:##例如    s="(]"
                    return False
        return len(stack)==0

复杂度分析

时间复杂度：O(n)，其中 n是字符串 s的长度。

空间复杂度：O(n+∣Σ∣)，其中 Σ 表示字符集，本题中字符串只包含 6 种括号，6∣Σ∣=6。栈中的字符数量为 O(n)，而哈希表使用的空间为 O(∣Σ∣)，相加即可得到总空间复杂度。

4 leetcode1047. 删除字符串中的所有相邻重复项

题目描述

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入：”abbaca”
输出：”ca”
解释：
例如，在 “abbaca” 中，我们可以删除 “bb” 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 “aaca”，其中又只有 “aa” 可以执行重复项删除操作，所以最后的字符串为 “ca”。

解题思路

充分理解题意后，我们可以发现，当字符串中同时有多组相邻重复项时，我们无论是先删除哪一个，都不会影响最终的结果。因此我们可以从左向右顺次处理该字符串。

而消除一对相邻重复项可能会导致新的相邻重复项出现，如从字符串abba 中删除 bb 会导致出现新的相邻重复项aa 出现。因此我们需要保存当前还未被删除的字符。一种显而易见的数据结构呼之欲出：栈。我们只需要遍历该字符串，如果当前字符和栈顶字符相同，我们就贪心地将其消去，否则就将其入栈即可。

本题要删除相邻相同元素，其实也是匹配问题，相同左元素相当于左括号，相同右元素就是相当于右括号，匹配上了就删除。类似于leetcode 20. 有效的括号

那么再来看一下本题：可以把字符串顺序放到一个栈中，然后如果相同的话 栈就弹出，这样最后栈里剩下的元素都是相邻不相同的元素了。

代码

def removeDuplicates(s):
    """
    :type s: str
    :rtype: str
    """
    stack=[]
    for i in s:
        if stack and i==stack[-1]:#栈不为空  当和栈顶元素相等时候，pop栈顶元素
            stack.pop()
        else:#否则元素入栈
            stack.append(i)
    return "".join(stack)

复杂度分析

时间复杂度：O(n)，其中 n是字符串的长度。我们只需要遍历该字符串一次。

空间复杂度：O(n) 或 O(1)，取决于使用的语言提供的字符串类是否提供了类似「入栈」和「出栈」的接口。注意返回值不计入空间复杂度。

5 1021. 删除最外层的括号

题目描述

有效括号字符串为空 “”、”(“ + A + “)” 或 A + B ，其中 A 和 B 都是有效的括号字符串，+ 代表字符串的连接。

例如，””，”()”，”(())()” 和 “(()(()))” 都是有效的括号字符串。
如果有效字符串 s 非空，且不存在将其拆分为 s = A + B 的方法，我们称其为原语（primitive），其中 A 和 B 都是非空有效括号字符串。

给出一个非空有效字符串 s，考虑将其进行原语化分解，使得：s = P_1 + P_2 + … + P_k，其中 P_i 是有效括号字符串原语。

对 s 进行原语化分解，删除分解中每个原语字符串的最外层括号，返回 s 。

示例 1：

输入：s = “(()())(())”
输出：”()()()”
解释：
输入字符串为 “(()())(())”，原语化分解得到 “(()())” + “(())”，
删除每个部分中的最外层括号后得到 “()()” + “()” = “()()()”。

解题思路

思路：遍历字符串，遇到左括号就入栈，遇到右括号就出栈，每次栈空的时候，都说明找到了一个原语，记录下每个原语的起始位置和结束位置，取原字符串在原语的起始位置+1到原语的结束位置的子串便得到原语删除了最外层括号的字符串，拼接，即可解出答案。sssss

这道题本身并不麻烦，主要是理解这句原语的含义：

如果有效字符串 s 非空，且不存在将其拆分为 s = A + B 的方法，我们称其为原语

其实就是每获取一组左右括号相等的搭配后，将左右括号各删除一个，并保存即可。
由于这道题目提供的用例都是满足括号匹配关系的内容，使得这道题的难度就更低了。

我们创建一个字符串用于接收每次获取的原语进行拼接
然后创建一个栈，开始循环s，进行栈的入栈操作，每次入栈的是s的下标
左括号直接入栈，右括号时弹出栈顶，并判断栈是否为空，为空则代表找到一对匹配内容
此时获取栈顶index以及当前循环的下标i，ret += s[left+1:i]（删除最外层的左右括号）即可。

代码

class Solution(object):
    def removeOuterParentheses(self, s):
        """
        :type s: str
        :rtype: str
        """
        ret=""
        stack=[]#记录索引
        for i in range(len(s)):
            if s[i]=='(':
                stack.append(i)
            else:
                left=stack.pop()
                if not stack:
                    ret+=s[left+1:i]
        return ret

1前言

链表和数组一样都是线性结构，但是数组是一段连续的存储空间，而链表空间不一定保证连续，而是可以存在于内存中未被占用的任意位置为临时分配的。因此如果要找第i个元素的值，是不能直接获取的，只能从链表首元素通过next指针进行查找。

每日一题的leetcode

排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。