1前言
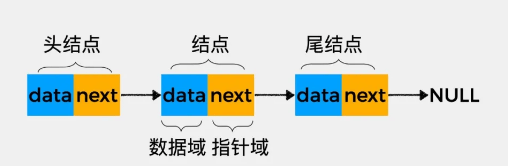
链表和数组一样都是线性结构,但是数组是一段连续的存储空间,而链表空间不一定保证连续,而是可以存在于内存中未被占用的任意位置为临时分配的。因此如果要找第i个元素的值,是不能直接获取的,只能从链表首元素通过next指针进行查找。 基于此,链表这种数据结构,除了要存储数据元素的信息外,还需要存储它的后继元素的存储地址。链表的组成结构如下图:
接着介绍下链表中几个重要概念:
结点——链表所占用的一个内存块,一个结点包括数据域和指针域两部分。数据域用于存储数据信息data,指针域用于存储下个结点的地址next,通常叫做后继指针。
头结点——链表中的第一个结点,只要知道了头结点在内存中的地址,就可根据其指针域存储的下一个结点的地址找到下一个结点。
尾结点——链表中的最后一个结点,由于是链表中的最后一个结点,它的指针域存储的不是下一个结点的地址而是NULL,以此来表示是链表的尾结点。
数组和链表对比
| 种类 | 优点 | 缺点 |
|---|---|---|
| 数组是一种连续存储线性结构,元素类型相同,大小相等 | 存取速度快 | 事先必须知道数组的长度;空间通常是有限制的;需要大块连续的内存块;插入删除元素的效率很低 |
| 链表是离散存储线性结构 | 空间没有限制;插入删除元素很快 | 节点的获取很慢 |
1.1链表分类
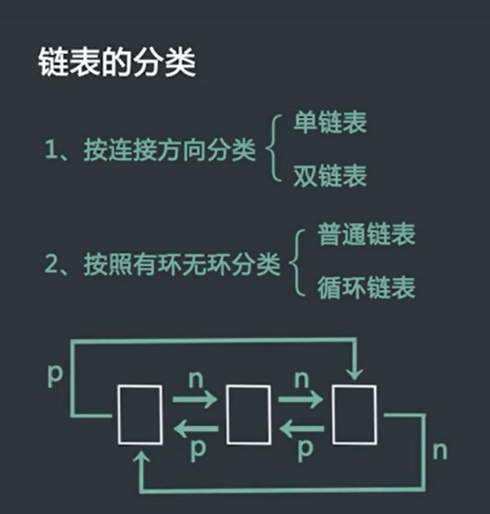
链表分类:
对于链表,如果用数组实现。那即是静态链表
链表按照连接方向分类分为:
- 单向链表,
- 一个节点有一个指针域属性,指向其后继节点,尾节点的后继节点为NULL。
- 双向链表
- 一个节点两个指针域属性,分别指向其前驱,后继节点
链表按照有无环分类:
1.2链表的基本操作
链表的题通常需要注意两点:
- 舍得用变量,千万别想着节省变量,否则容易被逻辑绕晕
- head 有可能需要改动时,先增加一个 假头为dummyhead,返回的时候直接取 假dummyhead.next,这样就不需要为修改 head 增加一大堆逻辑了。
1.2.1 向链表指定位置添加新的结点
我们看下如何向链表的指定位置增加一个节点node。
由于链表的每个节点都存储了下一个节点的指针,因此,要想在指定位置增加一个节点node,就需要知道指定位置的前一个节点。首先明确下几个变量的含义:
- 变量prev——表示前一个节点,比如节点2的前一个节点就是节点1。
- 变量head——表示头结点所在位置。
- 变量node——表示要添加的节点。
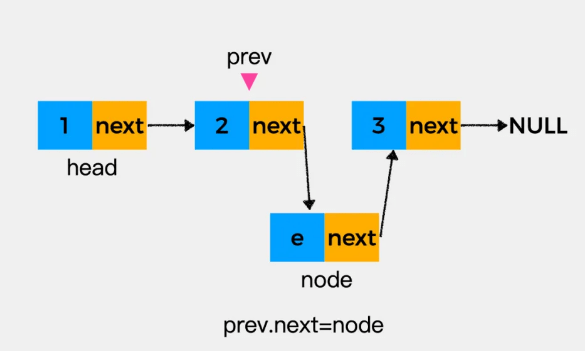
如何将结点node添加到结点3所在的位置。
(1)首先,将变量prev向后移动一个位置,指向结点3的前一个结点2所在的位置。
(2)将结点node的后继指针指向变量prev所指向结点的下一个结点,即node.next=prev.next
(3) 接着将变量prev所指向的结点的后继指针next指向node结点,即prev.next=node。这时,就将结点node添加到了原来结点3所在的位置。
特殊的,如果需要将节点node插入head前,成为新的头节点要怎么做?
这时就要介绍一个链表操作中常用的一个方法了:设置虚拟头结点dummyHead,来简化操作难度。
所谓虚拟头结点就是一个只存储下一个结点指针地址但不存储任何元素信息的节点。虚拟头结点的示例如下图,在有了虚拟头结点后,在向链表的头结点head所在位置添加元素时,操作方式就和向链表其它位置添加元素统一起来了。
时间复杂度
如果是向链表头添加结点,则只需将新的结点的后继指针指向当前链表的头结点即可,时间复杂度是O(1);
如果是向链表末尾添加结点,则需从头遍历链表直到尾部结点,因此此时的时间复杂度是O(n);
如果是向链表任意位置添加结点,那么平均来看时间复杂度就是O(n)。
1.2.2 删除链表指定位置的结点
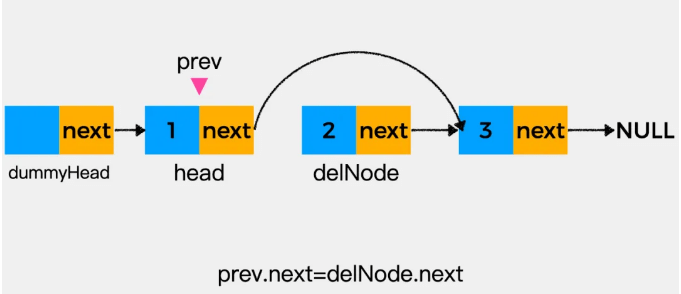
删除链表指定位置的结点,还是借助虚拟头结点来简化操作。如下图,假设要删除链表中第二个结点2。
- 首先,将变量prev向后移动一个位置,指向待删除结点的前一个结点。
- 接着,执行语句prev.next=delNode.next,即将变量prev所指向结点的后继指针next指向待删除结点的下一个结点
- 最后,执行delNode.next=null就可将待删除结点从链表中释放 最后,执行delNode.next=null就可将待删除结点从链表中释放
class Solution {
public ListNode deleteNode(ListNode head, int val) {
ListNode dummy=new ListNode();
dummy.next=head;
ListNode curr=dummy;
while(curr!=null&&curr.next!=null){//如果不加first != null,当需要删除的是最后一个节点时,就会有空指针异常
if(curr.next.val==val){
curr.next=curr.next.next;
}
curr=curr.next;
}
return dummy.next;
}
}复杂度分析
- 如果是删除头结点,则虚拟头结点就是头结点的前一个结点,因此时间复杂度是O(1);
- 如果是删除链表末尾添加结点,则需从头遍历链表直到尾部结点的前一个结点,因此此时的时间复杂度是O(n);
- 如果是删除链表中任意结点,那么平均来看时间复杂度就是O(n)。
1.3 链表相关题目
| 题号 | 题目 | 难度 |
|---|---|---|
| leetcode 21 | 合并两个有序链表 | 简单 |
| leetcode 203 | 移除链表元素 | 简单 |
| leetcode 206 | 反转链表 | 简单 |
| leetcode 92 | 反转链表 II | 中等 |
| leetcode 141 | 环形链表 | 简单 |
| leetcode 142 | 环形链表II | 中等 |
| 剑指 Offer 22 | 链表中倒数第k个节点 | 简单 |
| leetcode 160/剑指 Offer 52 | 两个链表的第一个公共节点 | 简单 |
| leetcode234 | 回文链表 | 简单 |
| leetcode 83 | 删除排序链表中的重复元素 | 简单 |
| leetcode 82 | 删除排序链表中的重复元素 II | 中等 |
| leetcode 61 | 旋转链表 | 中等 |
| leetcode 86 | 分隔链表 | 中等 |
2 leetcode21.合并两个有序链表
题目描述
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例1:
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
方法一:递归法
递归法注意输入是什么 输出是什么 需要关注两个点:终止条件和如何递归
思路
我们可以如下递归地定义两个链表里的 merge 操作(忽略边界情况,比如空链表等):
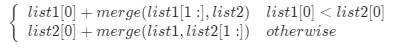
也就是说,两个链表头部值较小的一个节点与剩下元素的merge操作结果合并。
终止条件:当两个链表都为空时,表示我们对链表已合并完成。
如何递归:我们判断 l1 和 l2 头结点哪个更小,然后较小结点的 next 指针指向其余结点的合并结果。(调用递归)
执行过程:
//(1,1):代表第一次进入递归函数,并且从第一个口进入,并且记录进入前链表的状态
merge(1,1): 1->4->5->null, 1->2->3->6->null
merge(2,2): 4->5->null, 1->2->3->6->null
merge(3,2): 4->5->null, 2->3->6->null
merge(4,2): 4->5->null, 3->6->null
merge(5,1): 4->5->null, 6->null
merge(6,1): 5->null, 6->null
merge(7): null, 6->null
return l2
l1.next --- 5->6->null, return l1
l1.next --- 4->5->6->null, return l1
l2.next --- 3->4->5->6->null, return l2
l2.next --- 2->3->4->5->6->null, return l2
l2.next --- 1->2->3->4->5->6->null, return l2
l1.next --- 1->1->2->3->4->5->6->null, return l1代码实现
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution(object):
def mergeTwoLists(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
if l1 is None:
return l2
elif l2 is None:
return l1
elif l1.val<l2.val:#l1的当前头节点值更小,所以只需比较l1的下一个和l2头节点
l1.next=self.mergeTwoLists(l1.next,l2)
return l1#为啥要返回?因为递归的依次返回上级的时候,需要用这个较小节点来赋值 x.next。
else:#l2的当前头节点值更小,所以只需比较l2的下一个和l1头节点
l2.next=self.mergeTwoLists(l1,l2.next)
return l2其实递归就是程序内部维护了一个栈。这个题就是每次都把最小值压入栈,最后出栈的时候,将所有数连在一起就可以了。说白了,就是用一个栈维护了顺序。最后的连接,当然是小的连小的,所以l1 小,就连到 l1,l2 小就连到 l2,最后先返回的,就是最小的头结点。
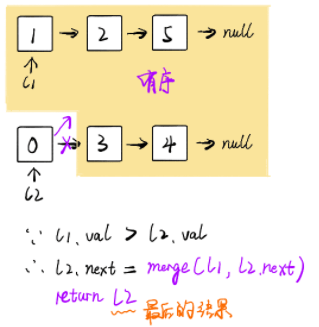
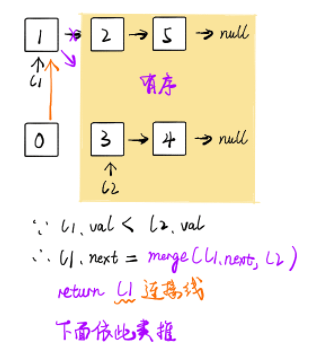
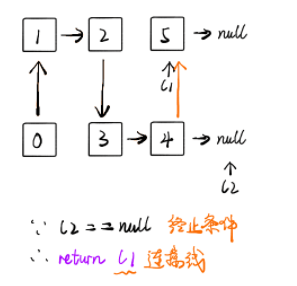
复杂度分析
如何计算递归的时间复杂度和空间复杂度呢? 力扣对此进行了 详细介绍 ,其中时间复杂度可以这样计算:
给出一个递归算法,其时间复杂度O(T) 通常是递归调用的数量(记作R) 和计算的时间复杂度的乘积(表示为 O(s))的乘积:O(T)=R∗O(s)
时间复杂度:O(m+n)。m,n为l1和l2的元素个数。递归函数每次去掉一个元素,直到两个链表都为空,因此需要调用 R=O(m + n)次。而在递归函数中我们只进行了 next 指针的赋值操作,复杂度为 O(1),故递归的总时间复杂度为 O(T) =R∗O(1)=O(m+n) 。
空间复杂度:O(m+n)
对于递归调用 self.mergeTwoLists(),当它遇到终止条件准备回溯时,已经递归调用了 m+n 次,使用了 m+n 个栈帧,故最后的空间复杂度为 O(m+n)。
方法二:迭代法
思路
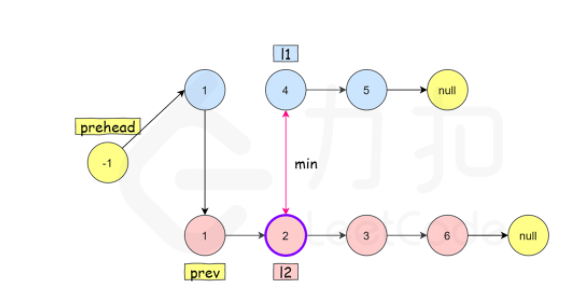
首先,我们设定一个哨兵节点 prehead ,这可以在最后让我们比较容易地返回合并后的链表。我们维护一个 prev 指针,我们需要做的是调整它的 next 指针。然后,我们重复以下过程,直到 l1 或者 l2 指向了 null :如果 l1 当前节点的值小于等于 l2 ,我们就把 l1 当前的节点接在 prev 节点的后面同时将 l1 指针往后移一位。否则,我们对 l2 做同样的操作。不管我们将哪一个元素接在了后面,我们都需要把 prev 向后移一位。
在循环终止的时候, l1 和 l2 至多有一个是非空的。由于输入的两个链表都是有序的,所以不管哪个链表是非空的,它包含的所有元素都比前面已经合并链表中的所有元素都要大。这意味着我们只需要简单地将非空链表接在合并链表的后面,并返回合并链表即可。
代码
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution(object):
def mergeTwoLists(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
prehead=ListNode(-1)
prev=prehead
while l1 and l2:
if l1.val<= l2.val:
prev.next=l1
l1=l1.next
else:
prev.next=l2
l2=l2.next
prev=prev.next
# 合并后 l1 和 l2 最多只有一个还未被合并完,我们直接将链表末尾指向未合并完的链表即可
prev.next = l1 if l1 is not None else l2
return prehead.next复杂度分析
时间复杂度:O(n + m),其中 n 和 m 分别为两个链表的长度。因为每次循环迭代中,l1 和 l2 只有一个元素会被放进合并链表中, 因此 while 循环的次数不会超过两个链表的长度之和。所有其他操作的时间复杂度都是常数级别的,因此总的时间复杂度为 O(n+m)。
空间复杂度:O(1)。我们只需要常数的空间存放若干变量。
3 leetcode203.移除链表元素
题目描述
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例1
输入:head = [1,2,6,3,4,5,6], val = 6
输出:[1,2,3,4,5]
解题思路
- 先设置一个虚拟头节点,dummyHead ,并指向头节点, dummyHead.next = head。
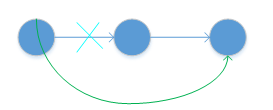
- 建立一个节点 cur 用来表示当前节点,cur始终指向要考虑的节点的前一个位置。如果 cur 的下一个节点不为空且下一个节点的节点值等于给定的 val ,则需要删除下一个节点的操作也是定式,即 cur.next = cur.next.next。如果 cur 的下一个节点的节点值不等于给定的 val,则保留下一个节点,将 cur 移动到下一个节点即可。
- 最终返回 dummyHead.next 即为删除操作后的头节点。
代码
class Solution(object):
def removeElements(self, head, val):
"""
:type head: ListNode
:type val: int
:rtype: ListNode
"""
dummy=ListNode()
dummy.next=head#记录头节点位置
p=dummy#遍历该链表指针
while p is not None:
if p.next and p.next.val==val:#相等则移除该元素
p.next=p.next.next#移除该元素
else:#否则继续往下找
p=p.next
return dummy.next复杂度分析
- 时间复杂度:O(n),其中 n 是链表的长度。需要遍历链表一次。
- 空间复杂度:O(1)。
4 leetcode206.反转链表
题目描述
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例1
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]方法一:双指针迭代
解题思路
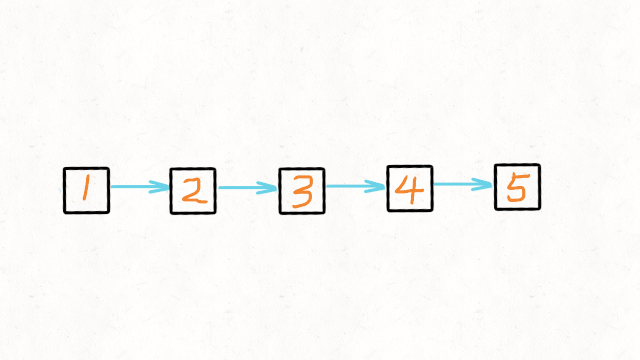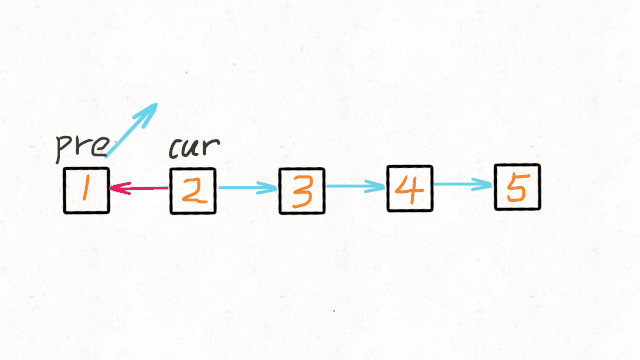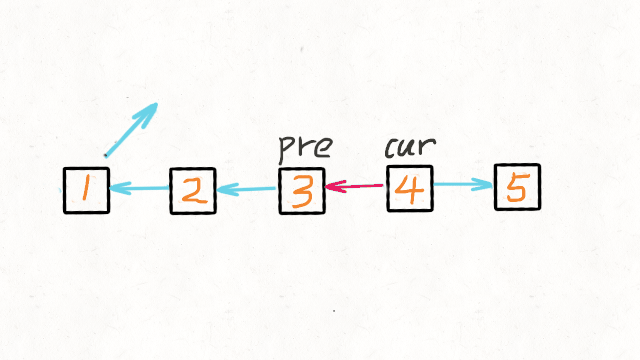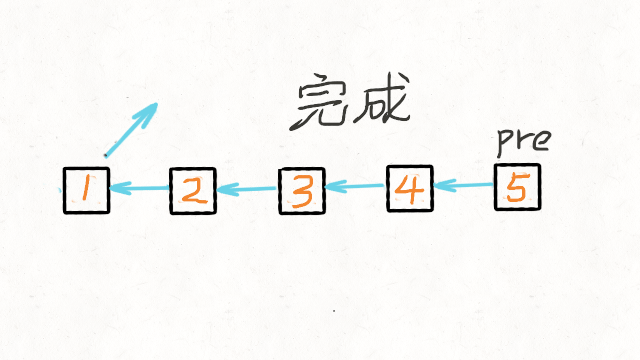
第一个指针叫 pre,最初是指向 null 的。
第二个指针 cur 指向 head,然后不断遍历 cur。
每次迭代到 cur,都将 cur 的 next 指向 pre,
然后 pre 和 cur 前进一位。
都迭代完了(cur 变成 null 了),pre 就是最后一个节点了。
代码
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution(object):
def reverseList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
pre=None#注意这里不要写成 pre=ListNode()
curr=head
while curr:
next=curr.next#保存当前节点的下一个值
curr.next=pre# 反转前节点curr反向指前一个元素pre
##curr和pre后移
pre=curr
curr=next
return pre复杂度分析
- 时间复杂度:O(n),其中 n是链表的长度。需要遍历链表一次。
- 空间复杂度:O(1)。
方法二:递归法
解题思路
递归版本稍微复杂一些,其关键在于反向工作。假设链表的其余部分已经被反转,现在应该如何反转它前面的部分?
假设链表为:
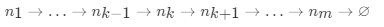
若从节点 n{k+1} 到 n{m}已经被反转,而我们正处于n{k}
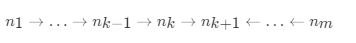
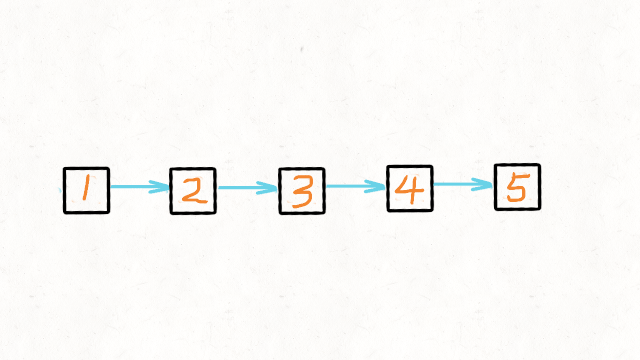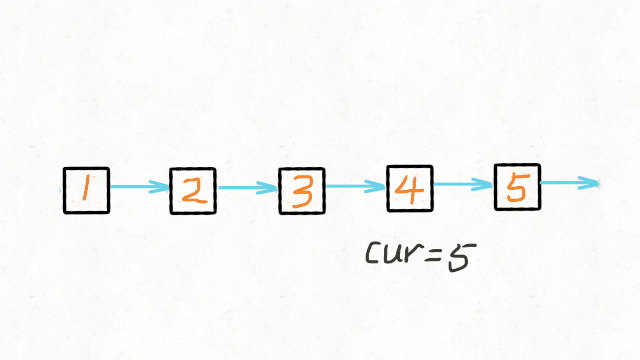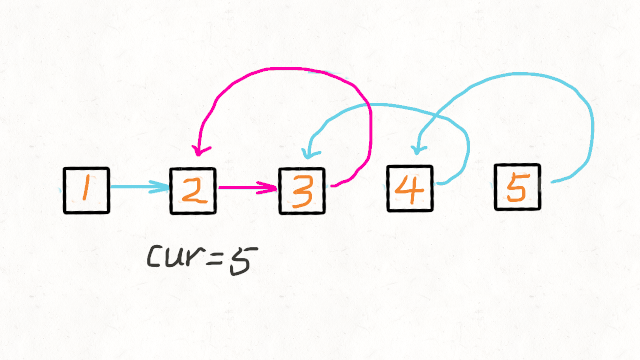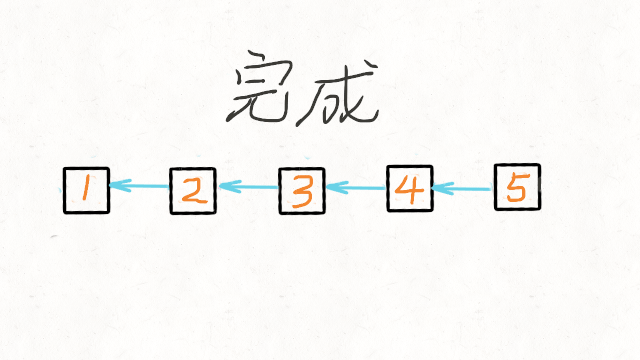
我们希望 n{k+1}的下一个节点指向n{k} 。
所以,nk.next.next=nk
需要注意的是 nk的下一个节点必须指向∅。如果忽略了这一点,链表中可能会产生环。详细图解参考
代码
class Solution(object):
def reverseList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if head is None or head.next is None:
return head
# 这里的cur就是最后一个节点
cur=self.reverseList(head.next)
head.next.next=head #局部反转 n{k+1}指向nk
head.next=None #nk--->n{k+1}断掉
# 每层递归函数都返回cur,也就是最后一个节点
return cur复杂度分析
时间复杂度:O(n),其中 n是链表的长度。需要对链表的每个节点进行反转操作。
空间复杂度:O(n),其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间,最多为 n 层
5 leetcode 92 反转链表 II
题目描述
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例1
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]方法一:穿针引线
解题思路
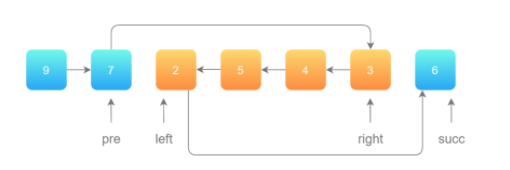
首先还需要记录 left 的前一个节点pre,和 right 的后一个节点succ。如图所示:
第 1 步:先将待反转的区域反转;
第 2 步:把 pre 的 next 指针指向反转以后的链表头节点,把反转以后的链表的尾节点的 next 指针指向 succ。
代码
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution(object):
def reverseBetween(self, head, left, right):
#############第 206 题,反转链表####
def reverseList(head):
pre=None
curr=head
while curr is not None:
next=curr.next#保存当前节点的下一个值
curr.next=pre# 反转 当前节点curr反向指前一个元素pre
##curr和pre后移
pre=curr
curr=next
#########################
dummy_node=ListNode(-1)
dummy_node.next=head#虚拟头节点指向原有头节点had
pre=dummy_node#初始位置为虚拟节点
# 第 1 步:找到left的前一个节点,所以需要从虚拟节点dummy处走left-1步
for _ in range(left-1):
pre=pre.next
right_node=pre
# 第 2 步:找到right节点,因此需要从pre再走right-left+1步
for _ in range(right-left+1):
right_node=right_node.next
# 第 3 步:切断出一个[left,right]子链表(截取链表)
left_node=pre.next#left节点
succ=right_node.next#找到right节点的后一节点
## # 注意:切断链接
pre.next=None
right_node.next=None
#第 4 步:同第 206 题,反转链表的子区间 [left,right]为[right,left]
reverseList(left_node)
#第5步:拼接到原来的链表中
pre.next=right_node
left_node.next=succ
return dummy_node.next复杂度分析
- 时间复杂度:O(N),其中 N是链表总节点数。最坏情况下,需要遍历整个链表,这里需要遍历2次链表,其中找到pre,left,right,succ的位置需要遍历一遍;其次翻转链表最坏的情况需要一次。
- 空间复杂度:O(1)。只使用到常数个变量。
方法二:一次遍历「穿针引线」反转链表(头插法)
解题思路

整体思想是:在需要反转的区间里,每遍历到一个节点,让这个新节点来到反转部分的起始位置。下面的图展示了整个流程。
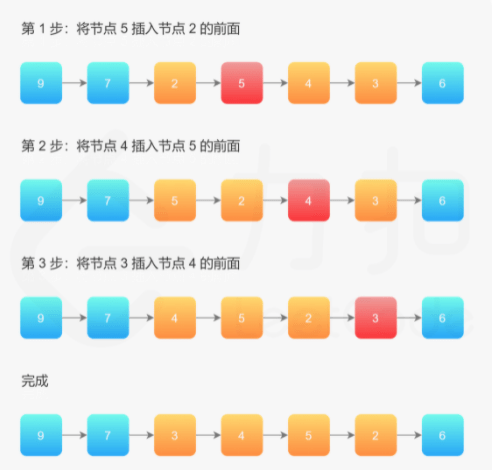
下面我们具体解释如何实现。使用三个指针变量 pre、curr、next 来记录反转的过程中需要的变量,它们的意义如下:
curr:指向待反转区域的第一个节点 left;
next:永远指向 curr 的下一个节点,循环过程中,curr 变化以后 next 会变化;
pre:永远指向待反转区域的第一个节点 left 的前一个节点,在循环过程中不变。
第 1 步,我们使用 ①、②、③ 标注「穿针引线」的步骤。
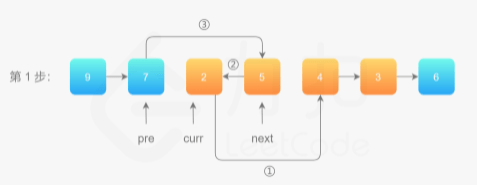
操作步骤:
先将 curr 的下一个节点记录为 next;
执行操作 ①:删除curr的next节点:把 curr 的下一个节点指向 next 的下一个节点;
执行操作 ②:插入curr前面–连接后面的curr:把 next 的下一个节点指向 pre 的下一个节点;
执行操作 ③:插入curr前面–连接前面的pre,把 pre 的下一个节点指向 next。
第 1 步完成以后「拉直」的效果如下:
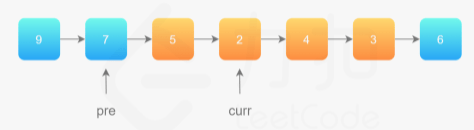
第 2 步,同理。同样需要注意 「穿针引线」操作的先后顺序。
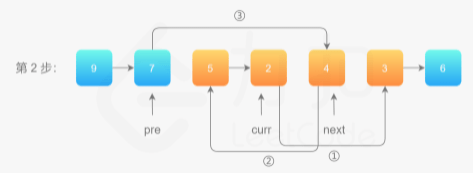
后面一直重复该步骤即可。
代码
class Solution(object):
def reverseBetween(self, head, left, right):
# ###########方法2 头插入法#需要遍历1次##############
dummy_node=ListNode(-1)
dummy_node.next=head#虚拟头节点指向原有头节点had
pre=dummy_node#初始位置为虚拟节点
# 第 1 步:找到left的前一个节点,所以需要从虚拟节点dummy处走left-1步
for _ in range(left-1):
pre=pre.next
curr = pre.next # 第一次为left节点
# 第 2 步:找到right节点,因此需要从pre再走right-left+1步
for _ in range(right-left):
next=curr.next
#####插入到left前面
curr.next=next.next#删除
##为什么next.next=curr是错的??
# 在第一次循环的时候结果是没问题的,但是在第二次循环时current就不再是previous指向的下一个值了,curr会后移一位变成pre.next.next 所以结果就错了。
next.next=pre.next#插入 连接后面的线
pre.next=next#插入 连接前面的线
#####为什么移动curr 不需要写curr=curr.next???
##因为将curr.next插入到curr前面,即pre的后面,插入完成后,curr位置直接后移了一个,curr.next是新的值
return dummy_node.next复杂度分析
- 时间复杂度:O(N),其中 N是链表总节点数。最多只遍历了链表一次,就完成了反转。
- 空间复杂度:O(1)。只使用到常数个变量。
6 剑指 Offer 22. 链表中倒数第k个节点
题目描述
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
示例:
给定一个链表: 1->2->3->4->5, 和 k = 2.
返回链表 4->5.
解题思路
第一时间想到的解法:
先遍历统计链表长度,记为 n ;
设置一个指针走 (n-k)步,即可找到链表倒数第 k个节点。
使用双指针则可以不用统计链表长度。也可想象为一个滑块,维护长度为k的滑块,当滑块的rifht为null,则left就是倒数第k个节点。如下图所示。
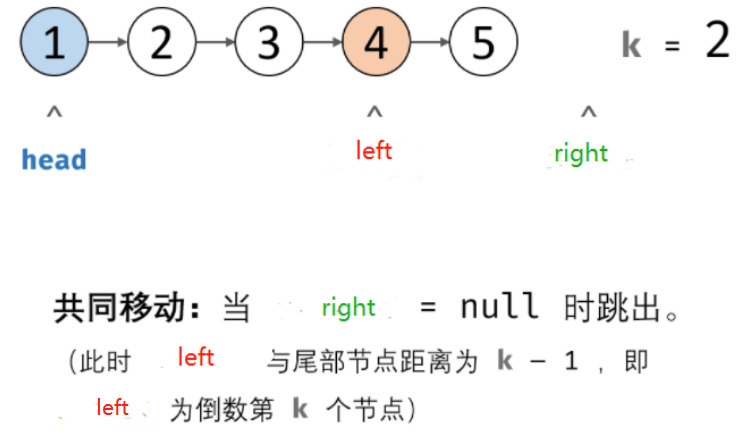
代码
class Solution(object):
def getKthFromEnd(self, head, k):
"""
:type head: ListNode
:type k: int
:rtype: ListNode
"""
left=head
right=head
###构造长度为k的滑块
for _ in range(k):
right=right.next
while right is not None:
##同步向右移动
left=left.next
right=right.next
return left#返回倒数第k个节点复杂度分析
时间复杂度 O(N) : N为链表长度;总体看, right走了 N 步, left走了 (N-k)步。
空间复杂度 O(1): 双指针 left, right使用常数大小的额外空间。
7 leetcode141. 环形链表
题目描述
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
示例 1:
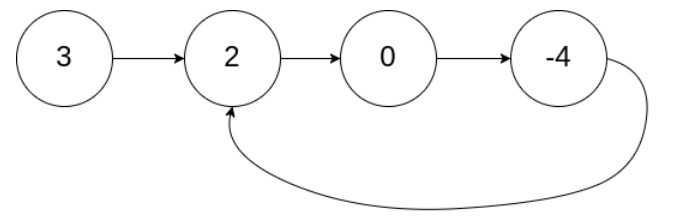
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点方法一:哈希表
解题思路
最容易想到的方法是遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
具体地,我们可以使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点,如果该节点已经存在于哈希表中,则说明该链表是环形链表,否则就将该节点加入哈希表中。重复这一过程,直到我们遍历完整个链表即可。
注意即使链表有重复的value值也没关系,因为哈希表中存的是地址,而不是val值。
代码
class Solution(object):
def hasCycle(self, head):
"""
:type head: ListNode
:rtype: bool
"""
######方法1 哈希表
record=set()
while head:
if head in record:#存在重复 则返回true
return True
record.add(head)
head=head.next复杂度分析
时间复杂度:O(N),其中 N 是链表中的节点数。最坏情况下我们需要遍历每个节点一次。
空间复杂度:O(N),其中 N是链表中的节点数。主要为哈希表的开销,最坏情况下我们需要将每个节点插入到哈希表中一次。
方法二:快慢指针
解题思路
本方法需要读者对「Floyd 判圈算法」(又称龟兔赛跑算法)有所了解。
假想「乌龟」和「兔子」在链表上移动,「兔子」跑得快,「乌龟」跑得慢。当「乌龟」和「兔子」从链表上的同一个节点开始移动时,如果该链表中没有环,那么「兔子」将一直处于「乌龟」的前方;如果该链表中有环,那么「兔子」会先于「乌龟」进入环,并且一直在环内移动。等到「乌龟」进入环时,由于「兔子」的速度快,它一定会在某个时刻与乌龟相遇,即套了「乌龟」若干圈。
我们可以根据上述思路来解决本题。具体地,我们定义两个指针,一快一满。慢指针每次只移动一步,而快指针每次移动两步。初始时,慢指针在位置 head,而快指针在位置 head.next。这样一来,如果在移动的过程中,快指针反过来追上慢指针,就说明该链表为环形链表。否则快指针将到达链表尾部,该链表不为环形链表。
对于为什么这个快指针走两步,慢指针走一步,必会在环内相遇?并且然后慢指针从开始重新走,另一个指针从快慢指针相遇位置走,这时每次都是走一步,两指针必会在环的入口处相遇。这是有数学公式可以证明的。
代码
class Solution(object):
def hasCycle(self, head):
###########方法2 快慢指针
if head is None or head.next is None:
return False
slow=head
fast=head
while fast is not None and fast.next is not None:
fast=fast.next.next#快指针走2步
slow=slow.next#慢指针走一步
if slow==fast:
return True#/先移动再判断,避免两个都在head还没移动的情况
return False#fast == null || fast.next == null复杂度分析
时间复杂度:O(N),其中 N是链表中的节点数。
当链表中不存在环时,快指针将先于慢指针到达链表尾部,链表中每个节点至多被访问两次。
当链表中存在环时,每一轮移动后,快慢指针的距离将减小一。而初始距离为环的长度,因此至多移动 N轮。
空间复杂度:O(1)。我们只使用了两个指针的额外空间。
8 leetcode142. 环形链表 II
题目描述
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
说明:不允许修改给定的链表。
进阶:你是否可以使用 O(1) 空间解决此题?
示例 1:
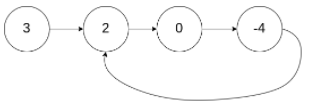
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。解题思路
我们使用两个指针,fast 与slow。它们起始都位于链表的头部。随后,slow 指针每次向后移动一个位置,而 fast 指针向后移动两个位置。如果链表中存在环,则fast 指针最终将再次与 slow 指针在环中相遇。
再理清步骤前,我们应该知道如下知识:如下图所示,设链表中环外部分的长度为 x。slow 指针进入环后,又走了y 的距离与 fast 相遇。此时,fast 指针已经走完了环的 n 圈(这里为了方便理解假设n=1,一般情况的推荐见详细原理),因此慢指针slow走过的距离为x+y,快指针fast走过的距离为x+y+z。因为快指针走过的距离是慢指针的2倍,则2(x+y)=x+y+z,从而x=z。
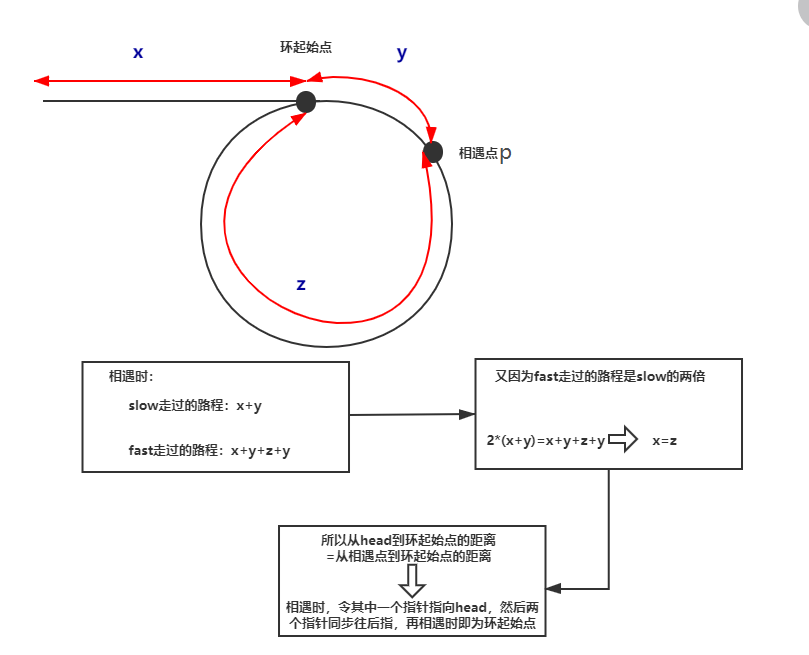
解题步骤:
(1)设置快慢指针都从head出发,快指针fast每次走2步,慢指针slow每次走1步,如果链表有环,则必然相遇在p点。
(2)第一次相遇后,将慢指针slow重新从链表的head出发,每次走一步;快指针保持在相遇点p处,继续前行但是每次都一步。(注意此时快慢指针同步前行)。由于前面推导出的x=z,则快慢指针一定会在环的入口处再次相遇。即得到了入环节点。(这里需要注意,当slow从head出发,fast从相遇点p出发,应该先判断fast是否等于head后,再同步向前走;因为如果先同步走再判断,会错过入环为head的情况)
代码
class Solution(object):
def detectCycle(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
fast=head
slow=head
while fast is not None and fast.next is not None:
fast=fast.next.next#快指针走两步
slow=slow.next#慢指针走1步
if fast==slow:
break
slow=head#慢指针重新从head走
while fast is not None and fast.next is not None:
if fast==slow:#注意这个要放Fast和slow同步移动的前面,因为环有可能在head上
return slow
#快慢指针同步走一步
fast=fast.next
slow=slow.next
return None复杂度分析
时间复杂度:O(N),其中 NN 为链表中节点的数目。在最初判断快慢指针是否相遇时,slow 指针走过的距离不会超过链表的总长度;随后寻找入环点时,走过的距离也不会超过链表的总长度。因此,总的执行时间为 O(N)+O(N)=O(N)。
空间复杂度:O(1)。我们只使用了slow,fast三个指针。
9 leetcode160. 相交链表
题目描述
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
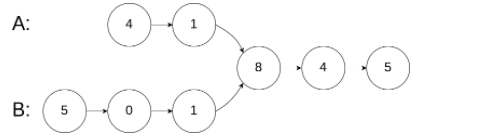
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at ‘8’
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
解题思路
本题目很容易想到使用哈希表,遍历A链表,存入哈希表中,再遍历B链表,发现重复值,即相交的点,时间复杂度为o(n),但是空间复杂度也为o(n)。
为了降低空间复杂度,可以使用双指针,我们需要做的事情是,让两个链表从同距离末尾同等距离的位置开始遍历。这个位置只能是较短链表的头结点位置。
为此,我们必须消除两个链表的长度差。
- 指针 pA 指向 A 链表,指针 pB 指向 B 链表,依次往后遍历
- 如果 pA 到了末尾,则 pA = headB 继续遍历
- 如果 pB 到了末尾,则 pB = headA 继续遍历
- 比较长的链表指针指向较短链表head时,长度差就消除了
如此,只需要将最短链表遍历两次即可找到位置,如下图所示。
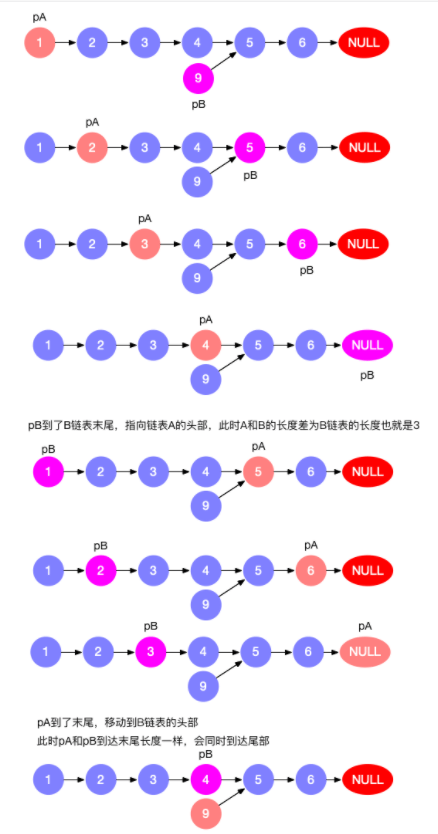
代码
class Solution(object):
def getIntersectionNode(self, headA, headB):
"""
:type head1, head1: ListNode
:rtype: ListNode
"""
a=headA
b=headB
while a!=b:
if a is None:
a=headB#a走完A链表,然后从headB再走
elif b is None:
b=headA#b走完B链表,然后从headA再走
else:#a,b同步往下走
a=a.next
b=b.next
return a#如果无交点,则a,b会同时指向None 复杂度分析
时间复杂度:O(m+n),其中 m 和 n 是分别是链表 headA 和headB 的长度。两个指针同时遍历两个链表,每个指针遍历两个链表各一次。
空间复杂度:O(1)。
10 leetcode 234 回文链表
题目描述
请判断一个链表是否为回文链表。
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true
解题思路-快慢指针法
本题较简单的方法是借助数组,将链表的值复制到一个数组中,在进行两段比较;但是这样因为使用了一个数组,空间复杂度为o(n),为了降低空间复杂度到o(1),我们使用快慢指针,起初都指向表头,快指针一次走两步,慢指针一次走一步,遍历结束时:
要么,slow 正好指向中间两个结点的后一个。
要么,slow 正好指向中间结点。
用 prev 保存 slow 的前一个结点,通过prev.next = null断成两个链表。
步骤如下:
1) 利用快慢指针,找到中间结点,即切割结点。并利用pre记录切割点的前一结点
2)将链表切割成两段,令pre.next=None
- 反转第二部分的链表 leetcode206题
4)开始比较两部分链表的val值,注意这里不能直接比较节点,应该比较节点的val值
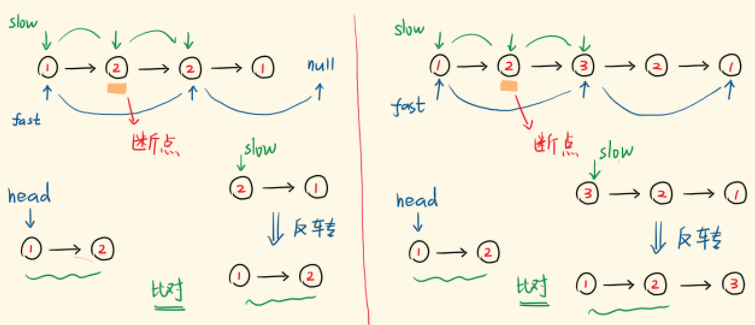
代码
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution(object):
def isPalindrome(self, head):
"""
:type head: ListNode
:rtype: bool
"""
###反转链表
def reverseList(head):
pre=ListNode()
curr=head
while curr is not None:
next=curr.next#保存当前节点的下一个值
curr.next=pre# 反转 当前节点curr反向指前一个元素pre
##curr和pre后移
pre=curr
curr=next
return pre
###第一步找到 切割点
fast=head
slow=head#慢指针,找到链表中间分位置,作为分割
pre=head # 记录慢指针的前一个节点,用来分割链表
while fast is not None and fast.next is not None:
pre=slow
fast=fast.next.next
slow=slow.next
###第二步 进行切割
pre.next=None#分割链表
##第三步 反转第二部分
cur1=head
cur2=reverseList(slow)#反转后半部分 总链表长度如果是奇数,cur2比cur1多一个节点
##第四步 开始两个链表的val的比较
while cur1:
if cur1.val!=cur2.val:
return False
cur1=cur1.next
cur2=cur2.next
return True复杂度分析
时间复杂度:O(n),其中 n指的是链表的大小。
空间复杂度:O(1)。我们只会修改原本链表中节点的指向,而在堆栈上的堆栈帧不超过 O(1)。
11 leetcode 83 删除排序链表中的重复元素
题目描述
存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除所有重复的元素,使每个元素 只出现一次 。
返回同样按升序排列的结果链表。
示例 1:
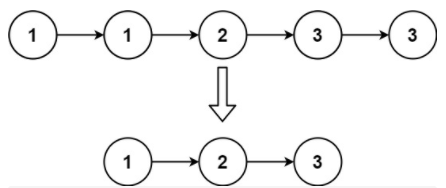
输入:head = [1,1,2,3,3]
输出:[1,2,3]解题思路
由于给定的链表是排好序的,因此重复的元素在链表中出现的位置是连续的,因此我们只需要对链表进行一次遍历,就可以删除重复的元素。
具体地,我们从指针cur 指向链表的头节点,随后开始对链表进行遍历。如果当前cur 与cur.next 对应的元素相同,那么我们就将cur.next 从链表中移除;否则说明链表中已经不存在其它与cur 对应的元素相同的节点,因此可以将cur 指向cur.next。
当遍历完整个链表之后,我们返回链表的头节点即可。
代码
class Solution(object):
def deleteDuplicates(self, head):
cur=head
while cur and cur.next:
if cur.val==cur.next.val:
#删除重复的next节点
cur.next=cur.next.next
#为什么跳过重复指针的时候,后边不再更新一下cur位置?即cur=cur.next
# 因为可能跳过重复位置后,cur和当前新的cur.next的值可能是相等的,所以还要再比较一次。
else:
cur=cur.next
return head复杂度分析
- 时间复杂度:O(n),其中 n是链表的长度。
- 空间复杂度:O(1)。
12 leetcode82删除排序链表中的重复元素 II
题目描述
存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除链表中所有存在数字重复情况的节点,只保留原始链表中 没有重复出现 的数字。
返回同样按升序排列的结果链表。
示例 1:
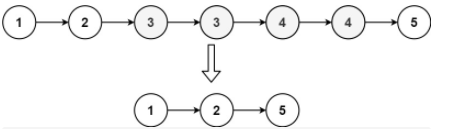
输入:head = [1,2,3,3,4,4,5]
输出:[1,2,5]
解题思路
由于给定的链表是排好序的,因此重复的元素在链表中出现的位置是连续的,因此我们只需要对链表进行一次遍历,就可以删除重复的元素。由于链表的头节点可能会被删除,因此我们需要额外使用一个哑节点(dummy node)指向链表的头节点。具体步骤如下:
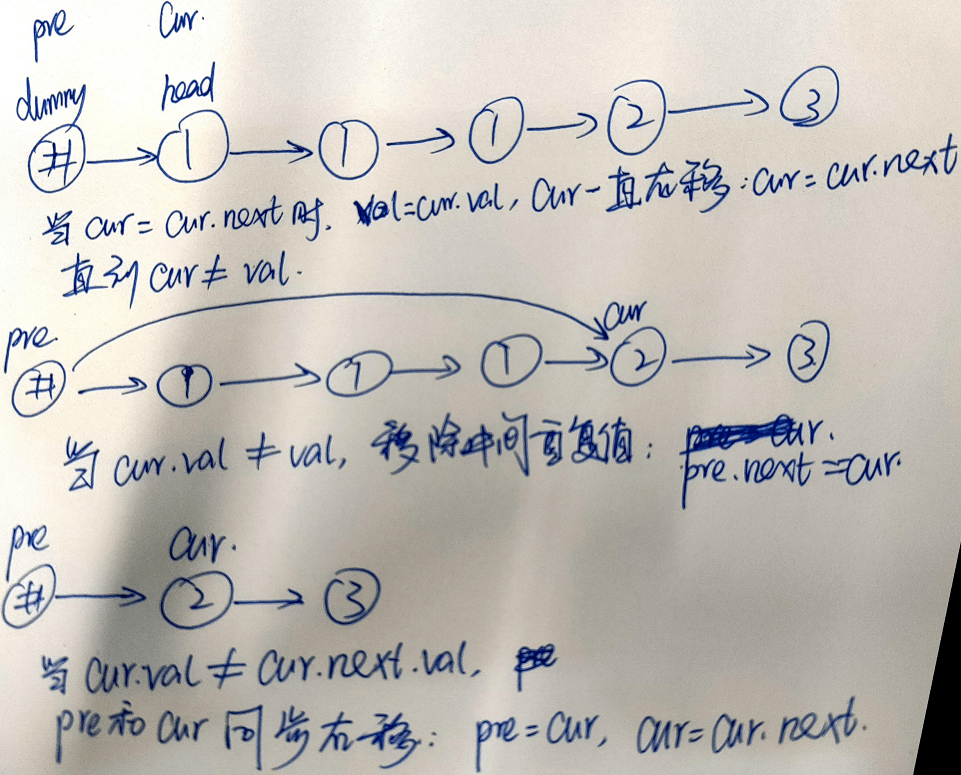
(1)我们从指针 pre指向链表的哑节点,cur指向head节点,随后开始对链表进行遍历。
(2)如果当前 cur与 cur.next对应的元素相同,那么我们就需要将 cur以及所有后面拥有相同元素值的链表节点全部删除。我们记下这个元素值val,随后不断将cur右移,直到其元素值不等于 xx 或者为空为止。此时,我们将链表中所有元素值为 xx 的节点全部删除:pre=cur。
如果当前 cur与 cur.next对应的元素不相同,只需要同步移动pre和cur即可。
代码
class Solution(object):
def deleteDuplicates(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
dummy=ListNode()
dummy.next=head
pre=dummy#保存游标前一个节点
cur=head
while cur and cur.next:
if cur.val==cur.next.val:#当前值与next值相等
val=cur.val#记录下重复值
###当前cur与cur.next重复,则pre和cur一直向右走,直到cur.next不重复
while cur.next is not None and cur.next.val==val:
#删除重复的cur与cur.next节点 包括当前节点
cur=cur.next
pre.next=cur.next#将pre的next指向cur的next,删除中间的重复值
cur=pre.next#cur删除了 #当前节点不是重复节点,pre来到cur的next位置 重新从pre.next走
else:#当前值与next值不相等
pre=cur
cur=cur.next#cur继续往下走
return dummy.next复杂度分析
- 时间复杂度:O(n),其中 n是链表的长度。
- 空间复杂度:O(1)。
13 leetcode61 旋转链表
题目描述
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
示例 1:
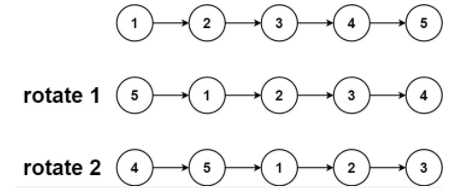
输入:head = [1,2,3,4,5], k = 2
输出:[4,5,1,2,3]解题思路
首位相接,再砍一刀:
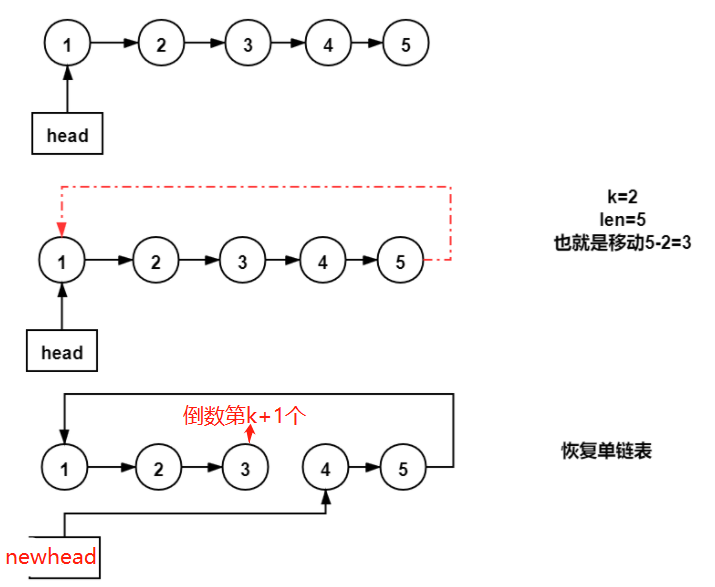
这道题目简单可以将链表每个节点向右移动 k 个位置转化为从倒数第k-1个元素处断开,将断开后的接到head前即可。更简单点就是 先将尾巴接到head上,再一刀从倒数第k+1个元素切开即可。具体步骤如下:
(1)计算链表长度n,并简化k:k=k%n
(2)将链表尾巴接到head上
(3)找到倒数第k+1个节点,切断:k+1.next=None(这里使用快慢指针也可以)
(4)返回新的头节点
代码
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution(object):
def rotateRight(self, head, k):
"""
:type head: ListNode
:type k: int
:rtype: ListNode
"""
if head is None or k==0:return head
n=0
cur=head
pre=head
###第一步:找到链表长度
while cur:
n=n+1
pre=cur
cur=cur.next
#第二步 K求余
k=k%n
#第三步 首位相连
pre.next=head
#第四步 找到切割点:即倒数第K个元素的前一个
cur=head
##找到切割点
for i in range(n-k-1):
cur=cur.next
#第五步 进行切割
newhead=cur.next#新的头节点
cur.next=None
return newhead复杂度分析
- 时间复杂度:O(N)
- 空间复杂度:O(1)
14 leetcode 86. 分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当保留两个分区中每个节点的初始相对位置。
示例1:
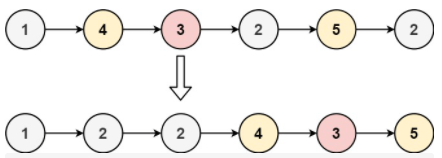
输入:head = [1,4,3,2,5,2], x = 3
输出:[1,2,2,4,3,5]示例 2:
输入:head = [2,1], x = 2
输出:[1,2]解题思路
只需要遍历链表的所有节点,小于x的放到一个小的链表中,大于等于x的放到一个大的链表中,最后再把这两个链表串起来即可。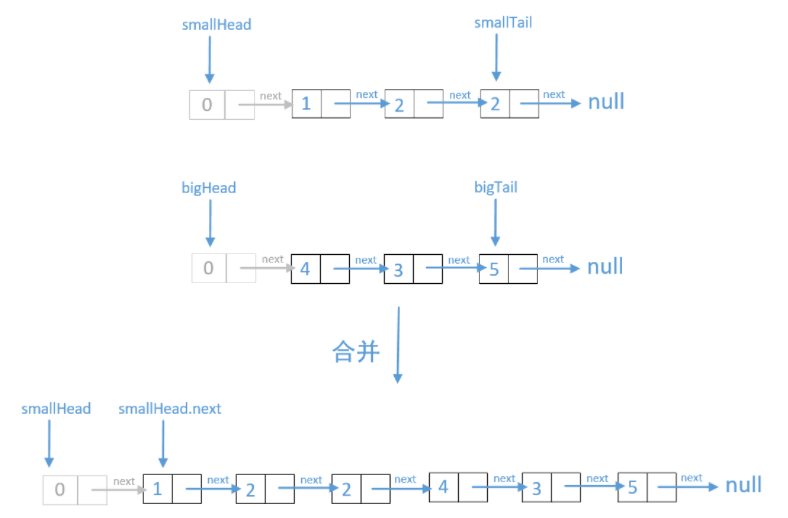
代码
class Solution(object):
def partition(self, head, x):
"""
:type head: ListNode
:type x: int
:rtype: ListNode
"""
#小链表的头
smallhead=ListNode()
#大链表的头
bighead=ListNode()
#小链表的尾巴
smalltail=smallhead
#大链表的尾巴
bigtail=bighead
while head:
if head.val<x:
# 如果当前节点的值小于x,则把当前节点挂到小链表的后面
smalltail.next=head
smalltail=smalltail.next
else:# 否则挂到大链表的后面
bigtail.next=head
bigtail=bigtail.next
head=head.next
#最后再把大小链表拼接在一块即可。
smalltail.next=bighead.next
bigtail.next=None
return smallhead.next复杂度分析
复杂度分析
- 时间复杂度: O(n),其中 n是原链表的长度。我们对该链表进行了一次遍历。
- 空间复杂度: O(1)。为啥空间复杂度是O(1)? 因为只生成了两个初始的头结点,之后的操作都是在原链表上进行的,head,small,big三个指针
参考文献
链表相关题目 超级棒 推荐
反转链表II解法 很详细
环距离公式推导 情况都考虑到了